Лабораторная работа №5 (10 класс)

Теория предсказывает, что при движении по наклонной плоскости ускорение тела не зависит от его массы. Действительно, пусть тело массой m под действием силы тяжести, силы реакции опоры и силы трения соскальзывает с наклонной плоскости с некоторым ускорением a. Пусть угол наклона плоскости к горизонту составляет α.

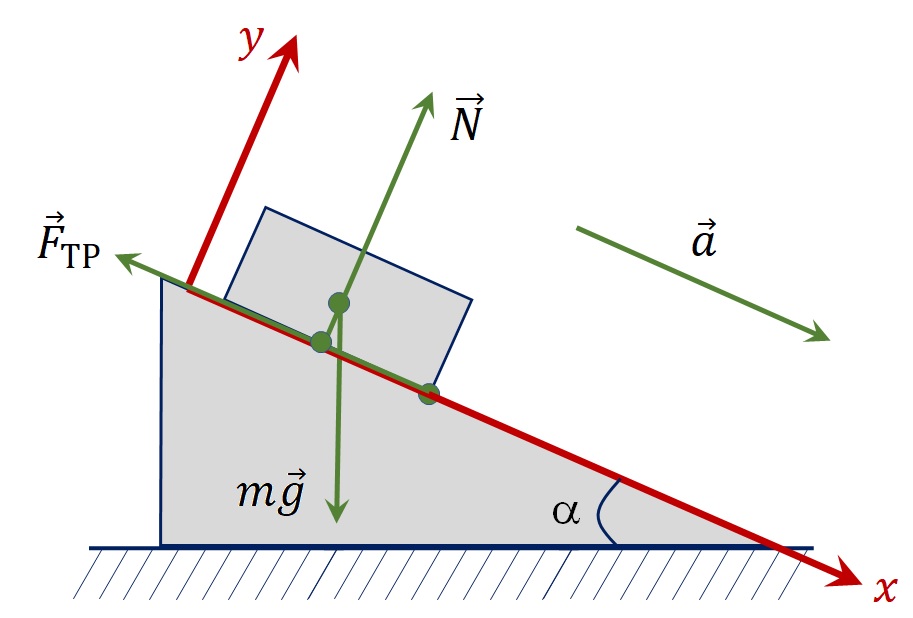
В соответствии со вторым законом Ньютона:

$$m\vec{g}+\vec{N}+\vec{F}_{ТР}=m\vec{a}$$

Запишем это уравнение в проекциях на оси Ox и Oy:

$$\begin{cases} & mg\cdot sin\alpha-F_{ТР}=ma \\ & N-mg\cdot cos\alpha=0 \end{cases}$$

Учитывая, что $$F_{ТР}=\mu N$$

получаем:

$$\begin{cases} & mg\cdot sin\alpha-\mu N=ma \\ & N-mg\cdot cos\alpha=0 \end{cases}$$

Подставим значение N из второго уравнения в первое: $$mg\cdot sin\alpha-\mu mg\cdot cos\alpha=ma$$

Откуда выражаем ускорение: $$a=g\left(sin\alpha-\mu cos\alpha \right)$$

Как видим, значение ускорения не зависит от массы бруска. В данной лабораторной работе вам предлагается это проверить экспериментально. Для этого необходимо провести два эксперимента по соскальзыванию бруска с наклонной плоскости. В этих двух экспериментах масса бруска должна отличаться.

Как можно измерить ускорение?

Путь, который совершает брусок при равноускоренном движении, вычисляется по формуле: $$S=v_{o}t+\frac{at^{2}}{2}$$

где:

• S — расстояние, которое проходит брусок, м;
• v₀ — начальная скорость бруска, м/c;
• t — время движения, с;
• a — ускорение, м/с².

Расстояние S измеряется линейкой. Время движения t измеряется электронным секундомером. Угол наклона рейки подбираем так, чтобы брусок соскальзывал с неё самостоятельно, без толчка. Поэтому его начальная скорость равна нулю. Получаем выражение для определения ускорения:
                                                            $$a=\frac{2S}{t^{2}}$$

Зная ускорение, можно рассчитать конечную скорость бруска. Действительно, скорость при равноускоренном движении вычисляется по формуле:
$$v=v_{0}+at$$

Начальная скорость равна нулю, поэтому выражение для конечной скорости принимает вид: $$v=at$$

Как вы думаете, получится ли экспериментально подтвердить равенство ускорений для двух брусков разной массы при их соскальзывании по наклонной плоскости? А если нет, то какие факторы на это могут повлиять?