Магический квадрат. Посчитаем?!

Как составить магический квадрат?

Начертим квадратную таблицу с одинаковым числом столбцов и строк. В получившиеся клетки впишем последовательные натуральные числа, начиная с единицы. Располагать числа в клетках будем так, чтобы сумма чисел в каждой строке, в каждом столбце и на обеих диагоналях была одинаковой. Такая таблица и называется магическим квадратом.

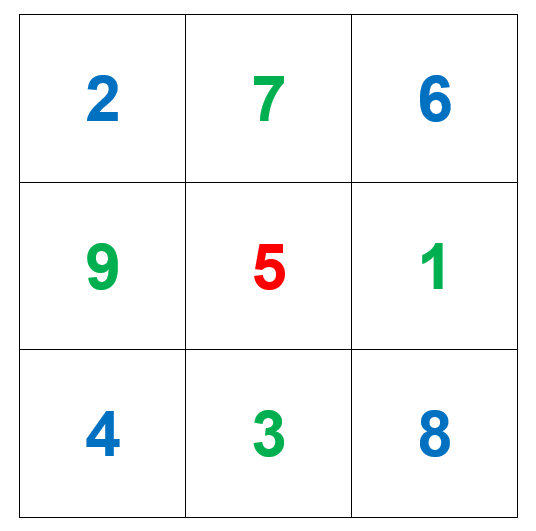
Число клеток в одном столбце (или одной строке) называется порядком магического квадрата. В магическом квадрате с порядком 3 числа можно разместить единственным образом (повороты, зеркальные отображения не считаются!). А ту сумму, которая получается при сложении чисел в каждом столбце, строке и диагонали, называют магической постоянной (или константой). Она обозначается М.

Как же найти постоянную для магического квадрата любого порядка? На самом деле очень просто: надо сложить все числа от 1 до n², а потом полученную сумму разделить на n. Например, квадрат порядка 3, n = 3. Всего клеток n²= 3² = 9. Сложим все числа: S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Разделим на n, S : n = 45 : 3 = 15. Значит, постоянная этого квадрата равна 15, М = 15. Даже можем найти, какое число будет стоять в центре: М : 3 = 15 : 3 = 5. Так можно поступить с любым квадратом. Правда, весело складывать числа от 1 до 49 для квадрата со стороной 7?! А если порядок ещё больше?

Тут нам на помощь придёт алгебра. Точнее, тот её раздел, который изучает числовые ряды. Оказывается, для нахождения суммы последовательных чисел от 1 до х есть формула S = х(х+1)/2. Для нахождения магической постоянной нам понадобится посчитать сумму последовательных чисел от 1 до n². То есть в нашей задаче x = n², а сумма равна S = n²(n² + 1)/2.

Таким образом, зная порядок квадрата n, можно вычислить его магическую постоянную: М = S/n = n(n² + 1)/2.

В данном проектном задании участникам предлагается составить свой магический квадрат.