Опубликовано
Метод вспомогательной окружности при решении планиметрических и стереометрических задач
Метод вспомогательной окружности при решении сложных нестандартных задач по геометрии очень быстро приводит к цели, позволяет решаемую задачу свести к элементарным задачам, решения которых известны или легко могут быть получены. Построение вспомогательной окружности помогает установить связь между данными и неизвестными элементами фигуры. По мнению Игоря Фёдоровича Шарыгина "Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою...”
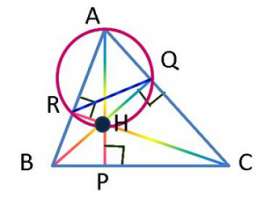
Протокол проведения работы
- Суть метода заключается в том, что при решении планиметрических и стереометрических задач, когда требуется установить связь между данными и искомыми величинами, нередко полезно около треугольника или четырехугольника описать окружность, после чего эти связи становятся более ощутимыми или даже очевидными. При решении таких задач полезно знание следующих теорем.Т1. Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:а) точки М и К расположены по одну сторону от прямой АВ и при этом ∠АМВ = ∠АКВ (рис. 1);б) точки М и К расположены по разные стороны от прямой АВ и при этом∠АМВ + ∠АКВ = 180 (рис. 2);то точки А, В, М, К лежат на одной окружности.
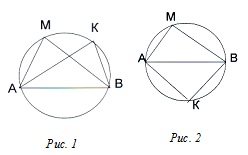Т2. Если ∠ АМВ = 90° и ∠АКВ = 90°, то точки А, В, М, К расположены на окружности с диаметром АВ.Сформулированные выше предложения можно назвать как свойства четырех точек окружности.Кроме того, для использования данного метода необходимы знания теорем о вписанных и центральных углах, и углах с вершиной внутри круга и с вершиной вне круга, углах между касательной к окружности и хордой, проведенной через точку касания, о свойствах вписанной в треугольник, четырёхугольник и описанной около треугольника, четырёхугольника окружности, и около каких четырёхугольников можно описать окружность,В процессе изучения метода вспомогательной окружности необходимо научиться выделять и использовать те признаки, наличие которых в задаче приводит к построению вспомогательной окружности и с ее помощью устанавливать связи между необходимыми объектами и величинами, определенными условием задачи. Тем более, что задачи на использование метода вспомогательной окружности, частые гости на ОГЭ и ЕГЭ. - Внимательно прочитайте условие задачи, выясните, что в ней требуется найти (первый взгляд на задачу). Ещё при анализе условия вы можете задумываться о возможности применить метод вспомогательной окружности. В качестве сигналов могут выступать следующие фразы: «опущены перпендикуляры…»,«проведены высоты…», «стороны (или прямые) перпендикулярны…». Как правило, в задачах идёт речь о двух перпендикулярностях. В контексте условия речь также может идти о двух углах, сумма заданных градусных мер которых, равна 180°.
- Аккуратно с помощью чертёжных инструментов постройте чертеж (конкретизация). На данном этапе выполните построение в соответствии с условием, одновременно конкретизируя и подводя под чертёж свои догадки относительно применения метода вспомогательной окружности.
- Выполните анализ чертежа. На данном этапе вы занимаетесь выявлением соответствующей ситуации (общей или частной), позволяющей обоснованно применить метод вспомогательной окружности.
- Обоснуйте выбор метода. После выбора конкретного случая вы должны провести его теоретическое обоснование, опираясь на общую возможность построения окружности по двум вписанным равным углам или же по вписанному в неё четырёхугольнику.
- Выполните дополнительное построение, то есть непосредственно постройте вспомогательную окружность.
- Проведите цепочку следствий. Окружность, как новый элемент позволяет расширить область возможных умозаключений, привнося видимость новых особенностей чертежа. Работая далее с углами в окружности в связи со всем чертежом задачи, выполняя поиск новых отношений, вы придёте к истинности доказываемого суждения.
- Оформите решение задачи, объясняя каждый ключевой момент.
- Заполните анкету проекта.
- Участвуйте в обсуждении результатов проекта. Например, вы можете в обсуждении спросить совета по решению задачи или предложить другой способ решения.
Техника безопасности
Не требуется.
