Сосчитаем листья
А вы знаете, что при очерёдном (спиральном) листорасположении количество листьев на один виток спирали постоянно для каждого растения?

Математические закономерности можно обнаружить во многих объектах и явлениях живой природы.
В этом проектном задании мы поговорим о том, какими математическими закономерностями выражается расположение листьев на стебле растения.
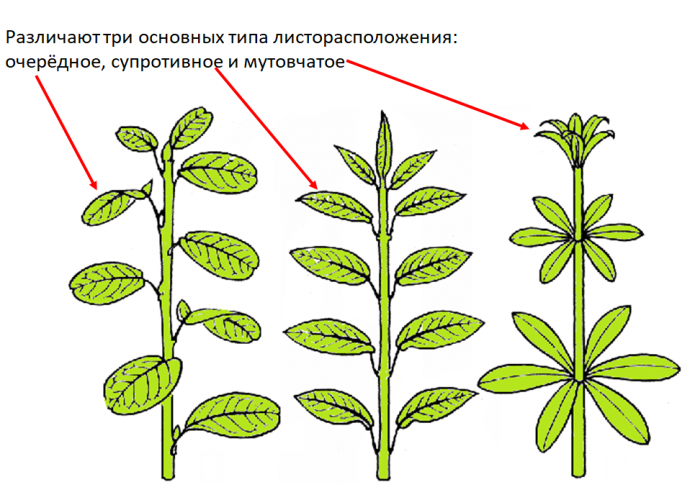
Есть три основных типа расположения листьев: очерёдное (спиральное), супротивное и мутовчатое. Все три типа можно описать, опираясь на два главных признака - это количество листьев в каждом узле и смещение листьев, находящихся в соседнем узле, выраженное в градусах.
Если вы посмотрите на стебель растения сверху, представляя себе проекцию листьев на плоскость, расположенную перпендикулярно стеблю, то смещение листьев соседних узлов можно описать как угол между радиусами, проведёнными через центр стебля и середину каждого из листьев. Этот угол называют углом расхождения.
У растений с супротивным листорасположением в каждом узле находится два листа. Листья следующего узла могут располагаться строго под листьями предыдущего, тогда при взгляде сверху мы увидим два продольных ряда листьев. Угол расхождения составляет 180°. Чаще листья каждого узла расположены между листьями соседних узлов, при этом при взгляде сверху мы увидим четыре продольных ряда листьев. Угол расхождения составляет 90°.

При мутовчатом листорасположении в каждом узле расположены три и более листьев, которые образуют мутовку листьев. Если у растения с трёхлистными мутовками листья одной мутовки располагаются между листьями соседних, то при взгляде сверху мы увидим 6 рядов листьев. Угол расхождения составляет 60°.
В этом проектном задании мы будем изучать только спиральное (очерёдное) листорасположение (оно более распространено в мире растений), которое подчиняется следующим закономерностям.
В каждом узле при этом листорасположении находится только один лист, причём лист следующего узла никогда не может быть точно под предыдущим, то есть угол расхождения не может равняться 0°. Однако рано или поздно при движении вниз или вверх по стеблю найдётся такой лист, который будет расположен точно под тем листом, с которого начат отсчёт. Поэтому, как и при супротивном и мутовчатом листорасположениях, при взгляде сверху можно увидеть продольные ряды листьев. Если соединить воображаемой линией основания листьев, то мы увидим, что это спираль, идущая вдоль стебля. Листья, расположенные на одном обороте спирали, составляют листовой цикл (кроме листа, расположенного точно над тем, с которого начался отсчёт).
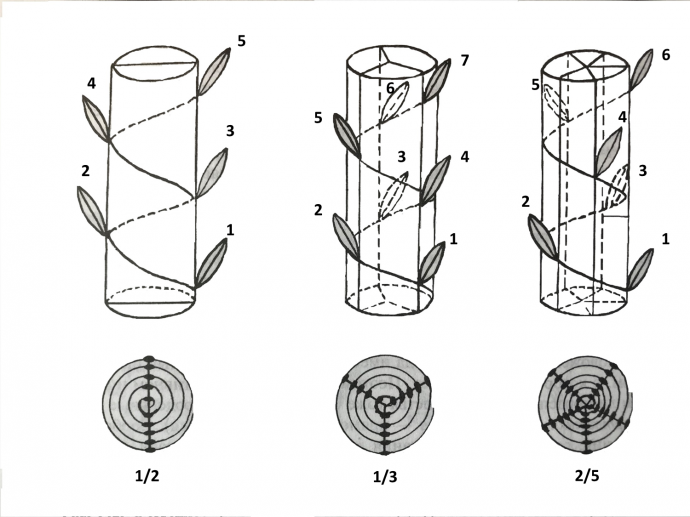
В самом простом варианте угол расхождения между соседними листьями составляет 180°. Спираль делает один оборот вокруг стебля от одного листа до другого, расположенного на той же линии. На один оборот спирали приходится 2 листа.
При угле расхождения, равном 120°, на один оборот спирали будет приходиться три листа.
Теперь представьте себе растение, у которого на одной линии будут находиться 1-й лист и 6-й лист. Тогда спираль будет совершать два оборота вокруг стебля от 1-го до 6-го листа. Во всех трёх случаях мы можем выразить отношение между числом оборотов спирали и количеством листьев в листовом цикле с помощью дроби, числитель которой будет соответствовать числу оборотов спирали, а знаменатель – числу листьев в листовом цикле.
Для растения, у которого на два оборота спирали приходится 5 листьев, как в последнем случае, эта дробь будет 2/5. Только таким образом мы можем выразить количество листьев, которое приходится на один оборот спирали.
Если мы исследуем значительное число разных растений с разным числом листьев, приходящихся на разное число оборотов спирали, то мы получим целый ряд дробей такого вида:
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34 и т.д.
Начиная с 2/5 каждая последующая дробь получается суммированием числителей и знаменателей двух предыдущих дробей. Такой ряд дробей называется рядом Фибоначчи.
Давайте попробуем обнаружить ряды Фибоначчи в живой природе!
